Chapter 6 Descriptive Statistics

6.1 Introduction to Statistics

6.1.1 Some Basic Terminologies Used in Statistics

i Population

The set of all possible elements in the universe of interest to the researcher

ii Sample

A Sample is a subset (a portion or part) of the population of interest
The sample must be a representative of the population of interest

iii Element

Element is an entity or object which the information is collected.
Eg: Student, household, farm, company, tomato plant

iv Variable

A variable is a feature characteristic which has different ‘values’ or categories for different elements (items/subjects/individuals)
Eg: Gender of client, brand of mobile phones, risk level, number of emails received per day, age of client, income of client

v Data

Data are measurements or facts that are collected from a statistical unit/entity of interest
We collect data on variables
Data are raw numbers or facts that must be processed (analysed) to get useful information.
We get information from data.
Eg:

Variable: Age (in years) of client

Data: 21, 45, 18, 32, 30, 22, 23, 27

Information:

The mean age is 27.25 years

The minimum age is 18 years

The range of ages is 18-45

The percentage of clients below 25 years of age: 50%

vi Statistic

Characteristic of a sample
The value which calculated based on sample data

vii Parameter

Characteristic of a population
The value which calculated based on population data

viii Census

When a researcher gathers data from the whole population for a given measurement, it is called a census

ix Sampling

When a researcher gathers data from a sample of the population for a given measurement, it is called sampling
The process of selecting a sample is also called sampling

Why take a sample instead of studying every member of the population ?

Prohibitive cost of census
Destruction of item being studied may be required
Not possible to test or inspect all members of a population being studied.

6.1.2 Branches of Statistics

i Descriptive Statistics

Descriptive statistics consists of organizing, summarizing and presenting data in an informative way.
The main purpose of descriptive statistics is to provide an overview of the data collected.
Descriptive statistics describes the data collected through frequency tables, graphs and summary measures (mean, variance, quartiles, etc.).

ii Inferential Statistics

In inferential statistics sample data are used to draw inferences (i.e. derive conclusions) or make predictions about the populations from which the sample has been taken.
This includes methods used to make decisions, estimates, predictions or generalizations about a population based on a sample.
This includes point estimations, interval estimation, test of hypotheses, regression analysis, time series analysis, multivariate analysis, etc.

6.1.3 Types of Variables

6.1.3.1 Qualitative / Quantitative Variables

i Qualitative variable (Categorical variable)

The characteristic is a quality.
The data are categories.
They cannot be given numerical values.
However, it may be given a numerical label
Qualitative variables are sometimes referred as categorical variables.
Eg:

Gender:

Age group:

Education level:

A/L stream:

Degree type:

Hair colour:

FIT student batch:

Undergraduate level:

Grade that you can obtain for CM 1110/ CM1130

ii Quantitative variable

The characteristic is a quantity
The data are numbers
Quantitative data require numeric values that indicate how much or how many.
They are obtained by counting or measuring with some scale
Eg:

Number of family members:

Number of emails received per day:

Weight of a student:

Age:

Credit balance in the SIM card:

Time remaining in class:

Temperature:

Marks

6.1.3.2 Discrete/ Continuous Variables

Quantitative variables can be classified as either discrete or continuous.

i Discrete Variables

Quantitative
Usually the data are obtained by counting
There are impossible values between any two possible values
Eg:

Number of family members:

Number of emails received per day:

ii Continuous Variables

Quantitative
Usually, the data are obtained by measuring with a scale
There are no impossible values between any two possible values.(any value between any two possible values is also a possible value)
i.e a continuous variable can take any value within a specified range.
Eg:

Weight of a student:

Age:

Credit balance in the SIM card:

Time remaining in class:

Temperature:

Marks

6.1.4 Scales of Measurements

There are four levels of measurements called, nominal, ordinal, interval and ratio.
Each levels has its own rules and restrictions
Different levels of measurement contains different amount of information with respect to whatever the data are measuring

i Nominal Scale

Qualitative
No order or ranking in categories.
These categories have to be mutually exclusive, i.e. it should not be possible to place an individual or object in more than one category
A name of a category can be substituted by a number, but it will be mere label and have no numerical meaning

ii Ordinal Scale

Qualitative
Categories can be ordered or ranked
A name of a category can be substituted by a number, but such a sequence does not indicate absolute quantities.
Difference between any two numbers on the scale does not have a numerical meaningful.
It cannot be assumed that the differences between adjacent numbers on the scale are equal.

iii Interval Scale

Quantitative
Data can be ordered or ranked
There is no absolute zero point. Zero is only an arbitrary point with which other values can compare
Difference between two numbers is a meaningful numerical value
Ration of two numbers is not a meaningful numerical value.

iv Ratio Scale

Quantitative
Highest level of measurement
There exist an absolute zero point (It has a true zero point)
Ratio between different measurements is meaningful

6.2 Presentation of Data

The sinking of the Titanic is one of the most infamous shipwrecks in history.

On April 15, 1912, during her maiden voyage, the widely considered “unsinkable” RMS Titanic sank after colliding with an iceberg. Unfortunately, there weren’t enough lifeboats for everyone onboard, resulting in the death of 1502 out of 2224 passengers and crew

Here’s a quick summary of our variables:

Variable Name	Description
PassengerID	Passenger ID (just a row number, so obviously not useful for prediction)
Survived	Survived (1) or died (0)
Pclass	Passenger class (first, second or third)
Name	Passenger name
Gender	Passenger Gender
Age	Passenger age
SibSp	Number of siblings/spouses aboard
Parch	Number of parents/children aboard
Ticket	Ticket number
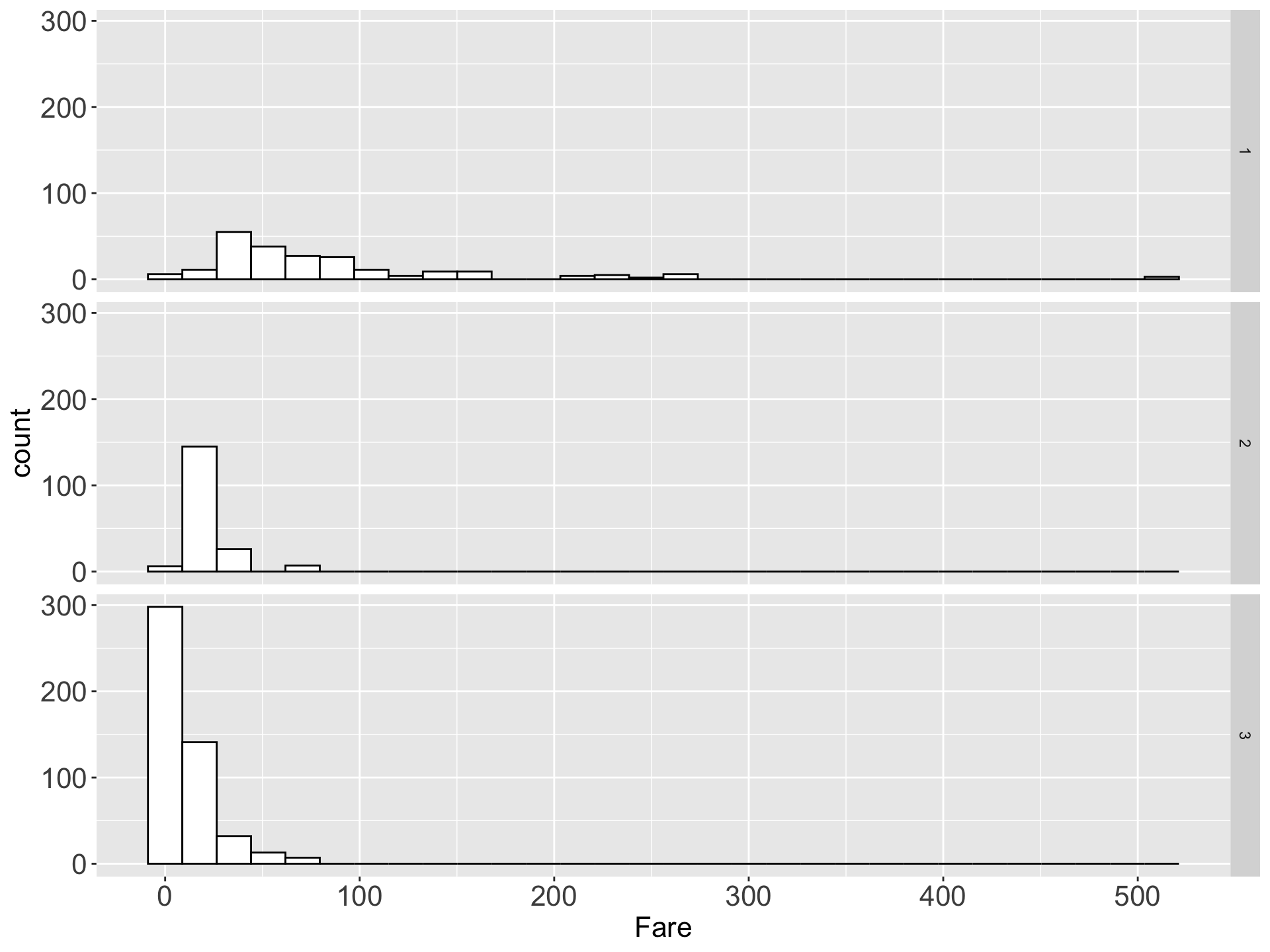
Fare	Fare
Cabin	Cabin
Embarked	Port of embarkation (S = Southampton, C = Cherbourg, Q = Queenstown)

6.2.1 Tabular Presentations of Data

Raw Data

Raw data are collected data that have not been organized numerically
Eg: Passenger age

##   PassengerId Survived Pclass
## 1           1        0      3
## 2           2        1      1
## 3           3        1      3
## 4           4        1      1
## 5           5        0      3
## 6           6        0      3
##                                                  Name    Sex Age SibSp Parch
## 1                             Braund, Mr. Owen Harris   male  22     1     0
## 2 Cumings, Mrs. John Bradley (Florence Briggs Thayer) female  38     1     0
## 3                              Heikkinen, Miss. Laina female  26     0     0
## 4        Futrelle, Mrs. Jacques Heath (Lily May Peel) female  35     1     0
## 5                            Allen, Mr. William Henry   male  35     0     0
## 6                                    Moran, Mr. James   male  NA     0     0
##             Ticket    Fare Cabin Embarked
## 1        A/5 21171  7.2500              S
## 2         PC 17599 71.2833   C85        C
## 3 STON/O2. 3101282  7.9250              S
## 4           113803 53.1000  C123        S
## 5           373450  8.0500              S
## 6           330877  8.4583              Q

##  [1] 22 38 26 35 35 NA 54  2 27 14  4 58 20 39 14 55  2 NA 31 NA 35 34 15 28  8
## [26] 38 NA 19 NA NA 40 NA NA 66 28 42 NA 21 18 14

An array

An array is an arrangement of raw numerical data in ascending or descending order of magnitude.
Eg: Passenger age

##  [1]  2  2  4  8 14 14 14 15 18 19 20 21 22 26 27 28 28 31 34 35 35 35 38 38 39
## [26] 40 42 54 55 58 66

Frequency Table (Frequency Distributions)

A frequency table (frequency distribution) is a listing of the values a variable takes in a data set, along with how often (frequently) each value occurs
frequency can be recorded as a
- frequency or count: the number of times a value occurs, or
- percentage frequency: the percentage of times a value occurs
Percentage frequency can be calculated as,

\[Percentage frequency = \frac{a}{b} \times100 \%\]

The objective of constructing a frequency table are as follows
- to organize the data in a meaningful manner
- to determine the nature or shape of the distribution
- to draw charts and graphs for the presentation of data
- to facilitate computational procedures for measures of average and spread
- to make comparisons between different data sets
There are two basic types of frequency tables
1. Simple frequency tables (Ungrouped frequency distribution)
2. Grouped frequency distribution

6.2.1.1 Simple frequency table (Ungrouped frequency distribution)

Each possible value or category is taken as a class
More suitable for
- Qualitative variables
- Discrete variables
Sometimes construct for continuous variables when there is a small number of possible values between the minimum and maximum.

Examples:

CASE I:

Example 1

The native countries of 56 students from a certain education institute are as follows:

##  [1] "SL" "BD" "SL" "SL" "SL" "SL" "IN" "SL" "SL" "SL" "BD" "SL" "SL" "SL" "IN"
## [16] "SL" "SL" "BD" "SL" "SL" "SL" "SL" "SL" "SL" "SL" "SL" "SL" "MD" "SL" "SL"
## [31] "SL" "SL" "SL" "SL" "PK" "MD" "PK" "SL" "SL" "SL" "SL" "SL" "PK" "MD" "SL"
## [46] "SL" "SL" "SL" "SL" "SL" "SL" "SL" "SL" "SL" "MD" "MD"

BD- Bangladesh, IN-India, MD-Maldives, PK-Pakistan, SL- Sri Lanka

Construct a frequency table

##  Native Country Count Percentage (%)
##      Bangladesh     3          5.357
##           India     2          3.571
##        Maldives     5          8.929
##        Pakistan     3          5.357
##       Sri Lanka    43         76.786
##           Total    56        100.000

CASE II:

Example 2

The grades of 30 students for Statistics are as follows:

##  [1] "B" "C" "B" "D" "B" "C" "C" "A" "B" "C" "C" "B" "E" "B" "B" "D" "D" "F" "B"
## [20] "D" "D" "A" "B" "A" "B" "C" "E" "A" "A"

Construct a frequency table

##  Grade Count Percentage (%)
##      A     5         17.241
##      B    10         34.483
##      C     6         20.690
##      D     5         17.241
##      E     2          6.897
##      F     1          3.448
##  Total    29        100.000

CASE III:

Example 3

The number of family members of a sample of undergraduates of Batch 19 are as follows:

##  [1] 7 5 3 4 5 4 3 6 4 4 5 2 7 4 5 6 4 4 3 5

Construct a frequency table

## # A tibble: 6 x 3
##   `Number of family members` Count `Percentage (%)`
##                        <dbl> <int>            <dbl>
## 1                          2     1                5
## 2                          3     3               15
## 3                          4     7               35
## 4                          5     5               25
## 5                          6     2               10
## 6                          7     2               10

CASE IV:

Example 4

The ages (in years) of a sample of undergraduates of Batch 19 are as follows:

##  [1] 21 22 22 23 22 24 24 23 21 22 23 22 22 23 21 21 22 23 22 23

Construct a frequency table

## # A tibble: 4 x 3
##   `Age (years)` Count `Percentage (%)`
##           <dbl> <int>            <dbl>
## 1            21     4               20
## 2            22     8               40
## 3            23     6               30
## 4            24     2               10

6.2.1.2 Grouped frequency distribution

A grouped frequency distribution (table) is obtained by constructing classes (or intervals) for the data and then listing the corresponding number of values in each interval.
Suitable for quantitative variables with large number of possible values in the range of data.
Note that when items have been grouped in this way, their individual values are lost.
When studying about frequency distributions it is very important to know the meaning of the following terms

i Class intervals

In a frequency distribution the total range of the observations are divided into a number of classes. Those are called class intervals
Eg: Class intervals: 10-14, 15-19, 20-24, …, 40-44

ii Class limits

Class limits are the smallest and largest piece of data value that can fall into a given class.
In the class interval 10-14, the end numbers, 10 and 14, are called class limits
The smaller number (10) is the lower class limit
The larger number (14) is the upper class limit

iii Class boundaries

Class boundaries are obtained by adding the upper limit of one class interval to the lower limit of the next-higher class interval and dividing by 2.
Class boundaries are also called True class limits
Class boundaries should not coincide with actual observations

Class interval	Class boundaries
10 - 14	9.5 – 14.5
15 - 19	14.5 – 19.5
20 - 24	19.5 – 24.5
25 - 29	24.5 – 29.5
30 - 34	29.5 – 34.5
35 - 39	34.5 – 39.5
40 - 44	39.5 – 44.5

iv The size or width of a class interval

The size or width of a class interval is the difference between the lower and upper class boundaries
It is also referred to as the class width, class size, or class length
Eg: The class width for the class 10-14 is = 14.5-9.5 = 5

v The class mark ( Midpoint of the class)

Midpoint of the class
Also called as class midpoint
$\text{Midpoint of the class} = \frac{\text{Lower limit} + \text{Upper limit}}{2}$

$\text{Midpoint of the class} = \frac{\text{Lower boundary} + \text{Upper boundary}}{2}$

vi Open class intervals

A class interval that, at least theoretically, has either no upper class limit or no lower class limit indicated is called an open class interval
For example, referring to age groups of individuals, the class interval “65 year and over” is an open class interval

Rules and Practices for constructing grouped frequency tables

Every data value should be in an interval
The intervals should be mutually exclusive
The classes of the distribution must be arrayed in size order.
The number of classes not less than 5 or not greater than 15 is recommended.
The following formula is often used to determine the number of classes: If n is the number of observations, then

\[\text{Number of classes} = \sqrt{n}\]

\[\text{Width of the class interval} = \frac{Range}{\sqrt{n}}= \frac{Min-Max}{\sqrt{n}}\]

Data should be represented within classes having limits which the data can attain
Classes should be continuous
By convention, the beginning of the interval is given the appropriate exact value, rather than the end.
Eg: intervals of 0-49, 50-99,100-149 would be preferred over the intervals 1-50, 51-100, 101-150 etc.
The number f observations falling into each category or class interval (class frequency) can be easily found using tally marks.

Examples:

In a grouped frequency distribution, class intervals can be constructed in different ways

Example 1

Class interval	Number of students
10 - 14	4
15 - 19	5
20 - 24	11
25 - 29	9
30 - 34	6
35 - 39	3
40 - 44	2

Example 2

Salary	Number of employees
0 – 1999	1
2000 – 3999	31
4000 – 5999	18
6000 – 7999	4
8000 – 9999	2
10000 - 11999	1
12000 – 13999	0
14000 – 15999	0
16000 – 17999	1
18000 -19999	1
20000-21999	1

Salary	Number of employees
0 – 1999	1
2000 – 3999	31
4000 – 5999	18
6000 – 7999	4
8000 – 9999	2
10000 - 15999	1
16000 – 21999	3
Total	60

Example 3

Salary	Number of employees
Less than 2000	1
2000 – 2999	11
3000 – 3999	20
4000 – 5999	18
6000 – 9999	6
Greater than or equal to 10000	4
Total	60

6.2.1.3 Two-way frequency table

Cross tabulation, Cross classification table, Contingency table, Two-way table
Display the relationship between two or more qualitative variables (categorical variables (nominal or ordinal))

## # A tibble: 2 x 4
##   Survived First Second Third
##   <chr>    <dbl>  <dbl> <dbl>
## 1 died        80     97   372
## 2 Survived   136     87   119

## # A tibble: 2 x 4
##   Survived First Second Third
##   <chr>    <dbl>  <dbl> <dbl>
## 1 died      0.37   0.53  0.76
## 2 Survived  0.63   0.47  0.24

6.2.2 Graphic Presentations of Data

A diagram is a visual form for presentation of statistical data.
The form of the diagram varies according to the nature of the data

6.2.2.1 Describing Qualitative Data

Bar chart / Pie chart
Suitable for
- Qualitative variables (nominal or ordinal)
- Discrete variables (when the number of bars or number of different values is small)

I Bar Chart

A bar graph uses bars to represent discrete categories of data
It can be drawn either on horizontal (more common) or vertical base
A rectangle of equal width is drawn for each category
The height (in vertical bar chart) or the length (in horizontal bar chart) of the rectangle is equal to the category’s frequency or percentage.

i Simple Bar Chart

Only one categorical variable can be presented
Often used in conjunction with simple frequency tables
The bars do not touch each other
The gaps between adjacent bars are same in length

Passenger class	Count	Percentage
First	216	24.242
Second	184	20.651
Third	491	55.107

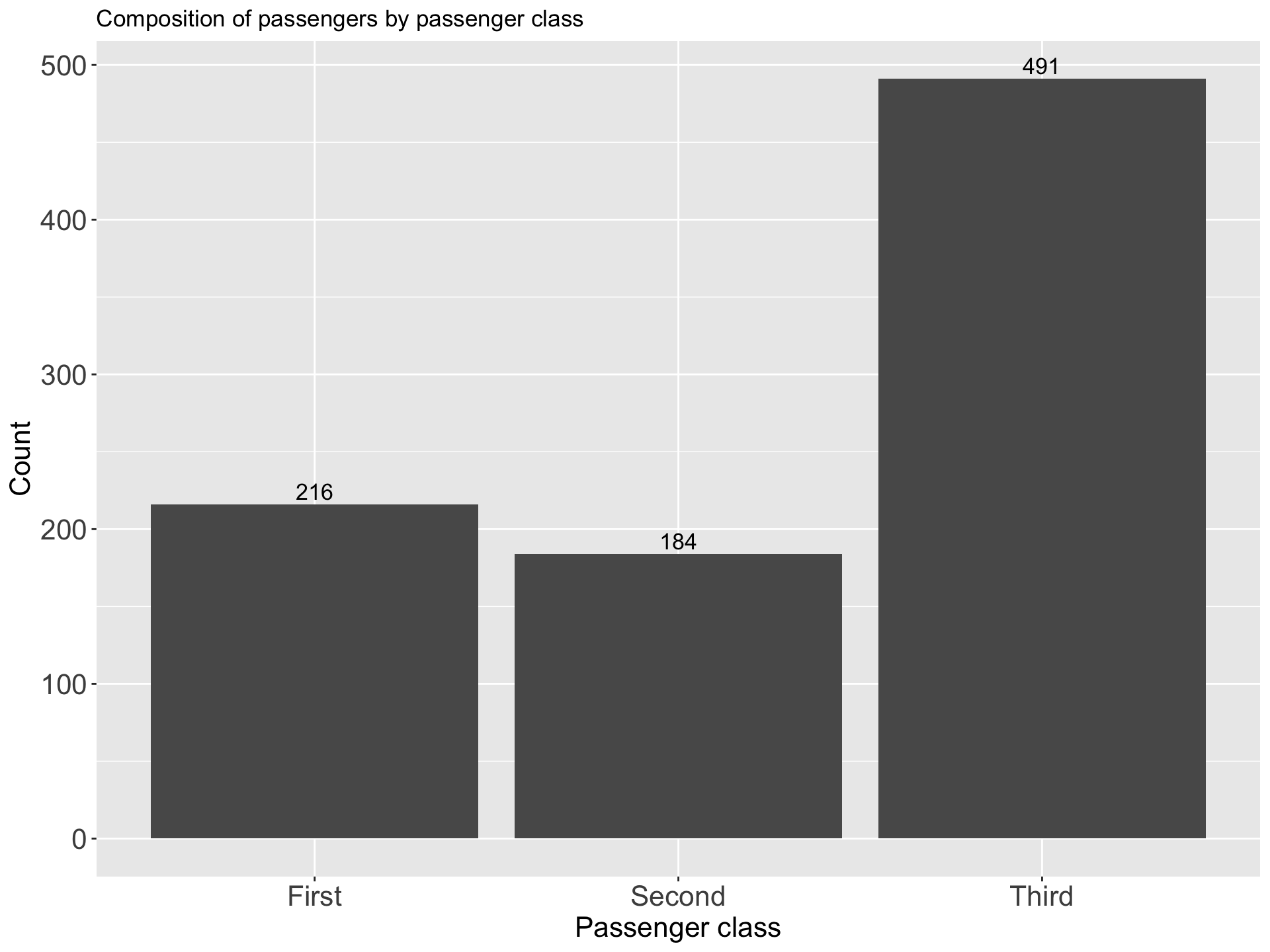
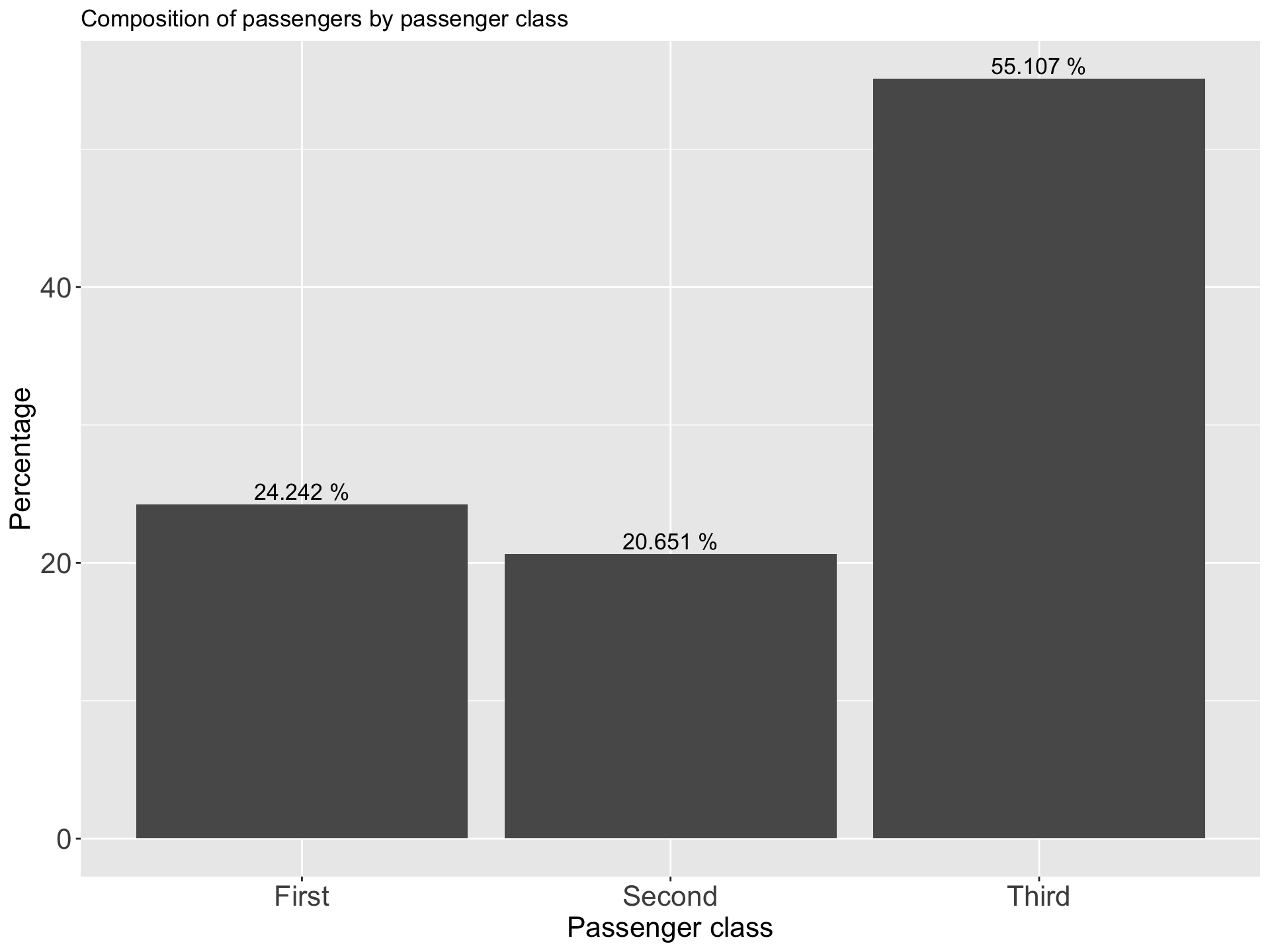
ii Component Bar Chart

Sub divided bar chart/ Stacked bar chart
Use to compare two or more qualitative variables (nominal or ordinal)
Often used in conjunction with two way tables
Start by drawing a simple bar chart with the total figures.
The bars are then divided into the component parts
Can be drawn on absolute figures or percentages
The various components should be kept in the same order in each bar
To distinguish different components from one another, different colours or shades can be used

Survived	First	Second	Third
died	80	97	372
Survived	136	87	119

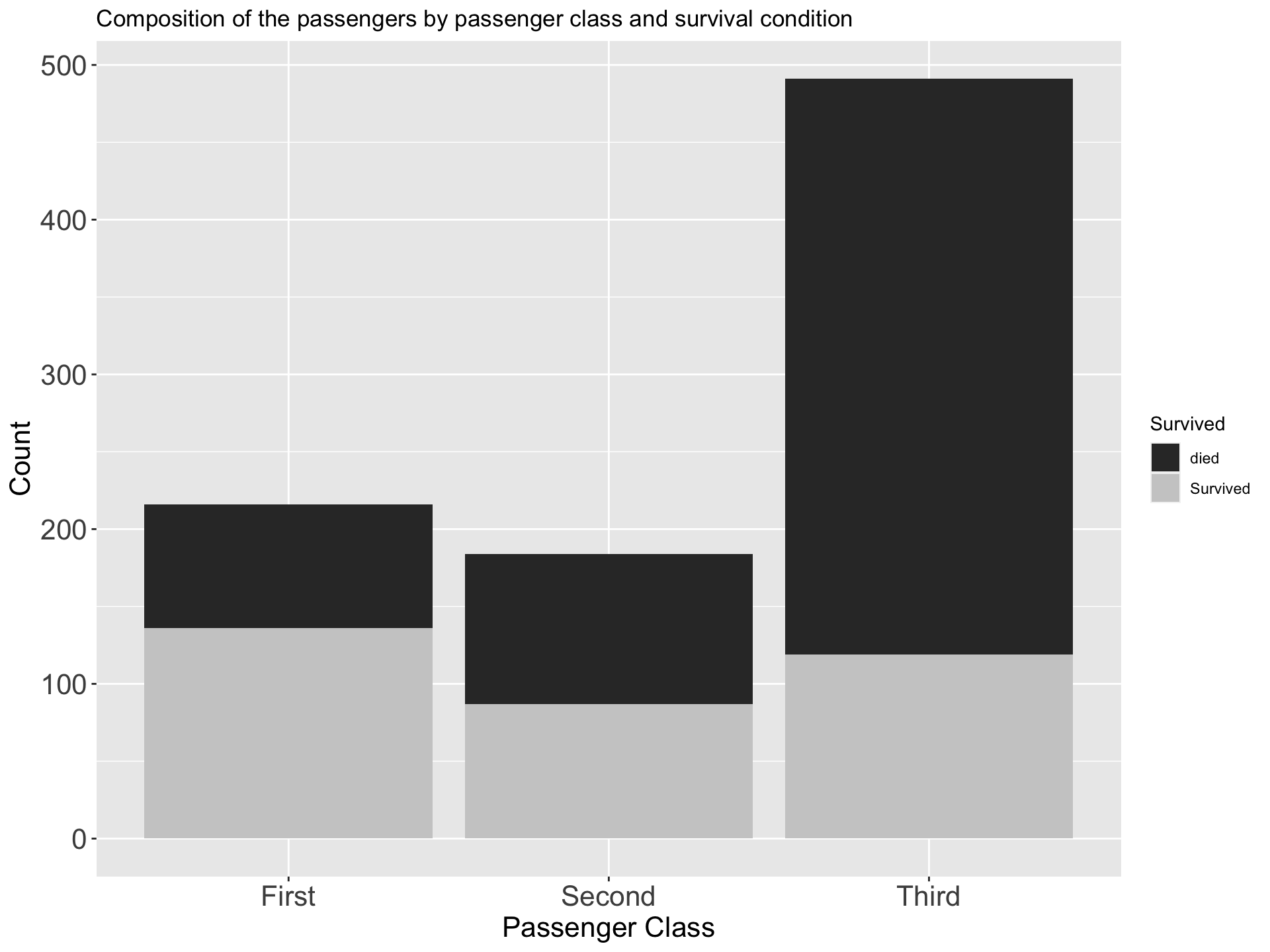
Percentage component bar chart

When sub-divided bar chart is drawn on percentage basis it is called percentage bar chart
The various components are expressed as percentage to the total
All bars are equal in height

Survived	First	Second	Third
died	0.3703704	0.5271739	0.7576375
Survived	0.6296296	0.4728261	0.2423625

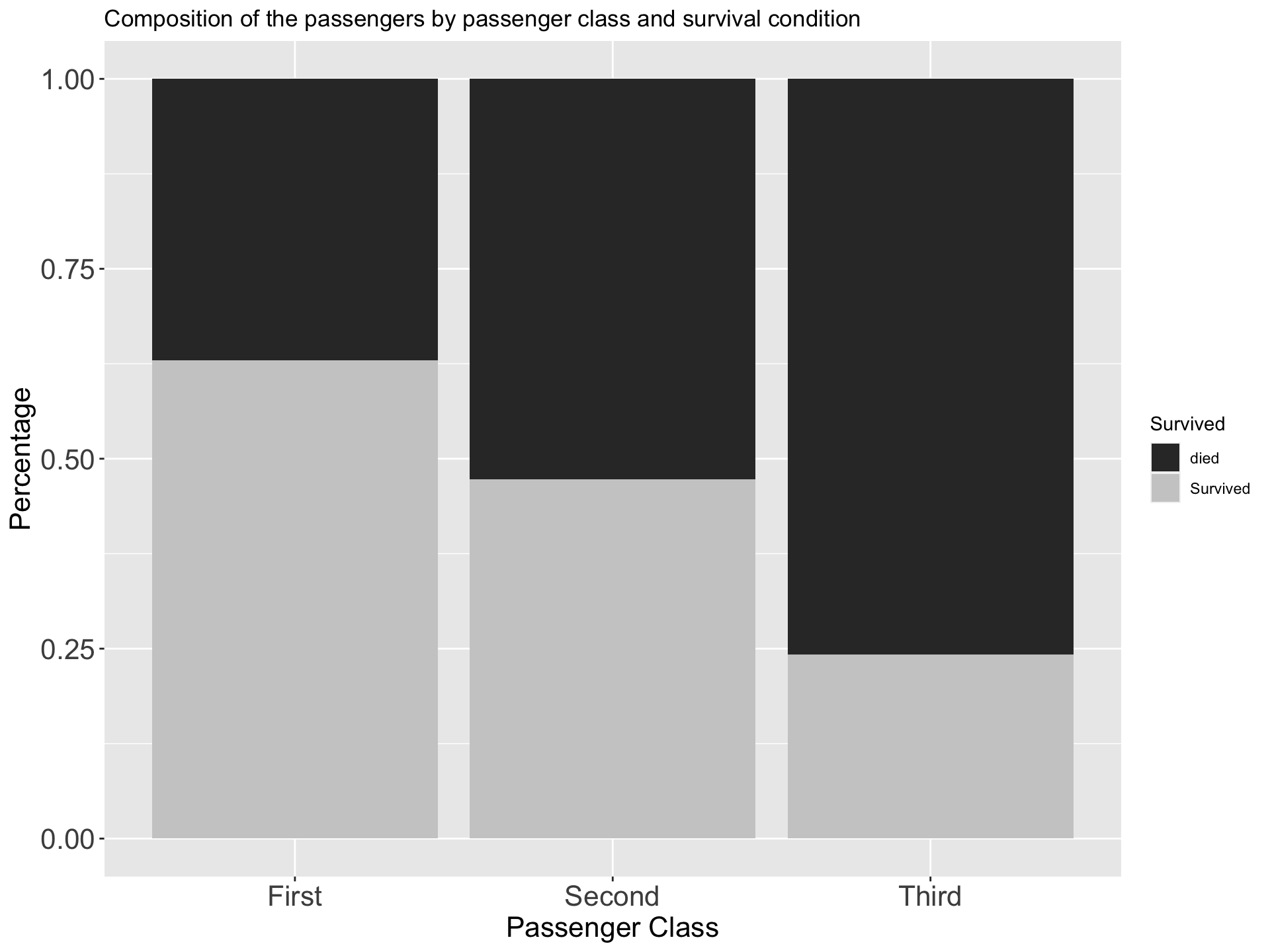
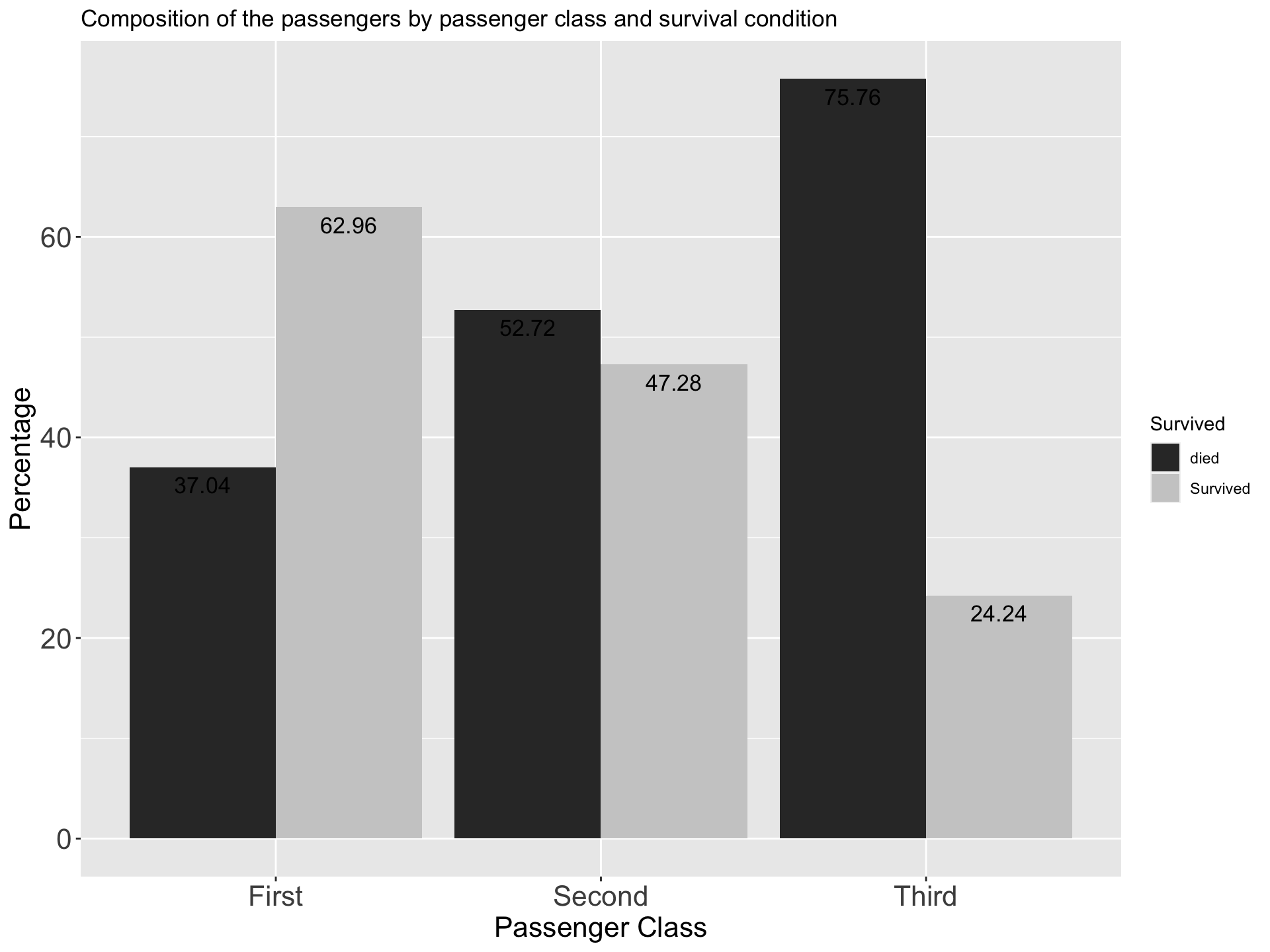
iii Multiple Bar Chart

Compound bar chart/ Cluster bar chart
Use to compare two or more qualitative variables (nominal or ordinal)
Often used in conjunction with two way tables
These bar charts are drawn side by side

Survived	First	Second	Third
died	37.04	52.72	75.76
Survived	62.96	47.28	24.24

6.2.2.2 Describing Quantitative Data

Histogram/ Dot plot / Box plot/ Scatter plot

II Histogram

Histogram looks similar to bar chart since it also has bars.
However, it is different from a bar chart in a number of aspects.
One main difference is that in the histogram, the bars are drawn attached to each other; there are no gaps between bars like in a bar chart.
Histogram is used to show the shape of the distribution of a continuous variable.
However, the histogram is also used for discrete variables when the data are grouped in to class intervals.
In a histogram, the area of a bar should be proportional to the frequency of the corresponding class.
If all the bars have the same width, then the height of a bar can represent the frequency.
The bar corresponding to a class interval should be drawn from the lower class boundary to the upper class boundary. In this way there will be no gaps between the bars.

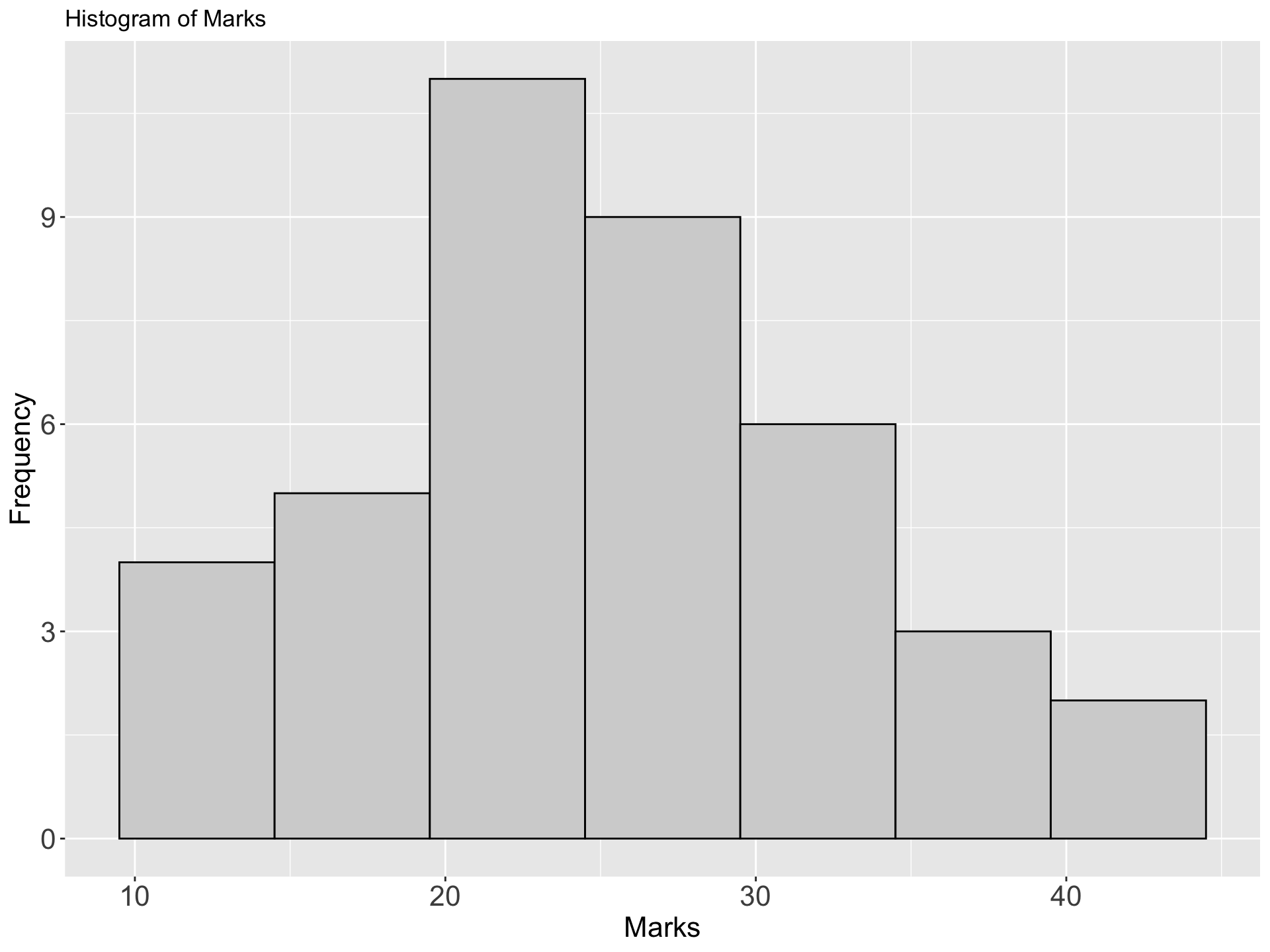
Example: The marks(out of 50) of a group of students are recorded in the accompanying table. Draw a histogram for the data

Marks	Number of students
10 - 14	4
15 - 19	5
20 - 24	11
25 - 29	9
30 - 34	6
35 - 39	3
40 - 44	2
Total	40

Example 2

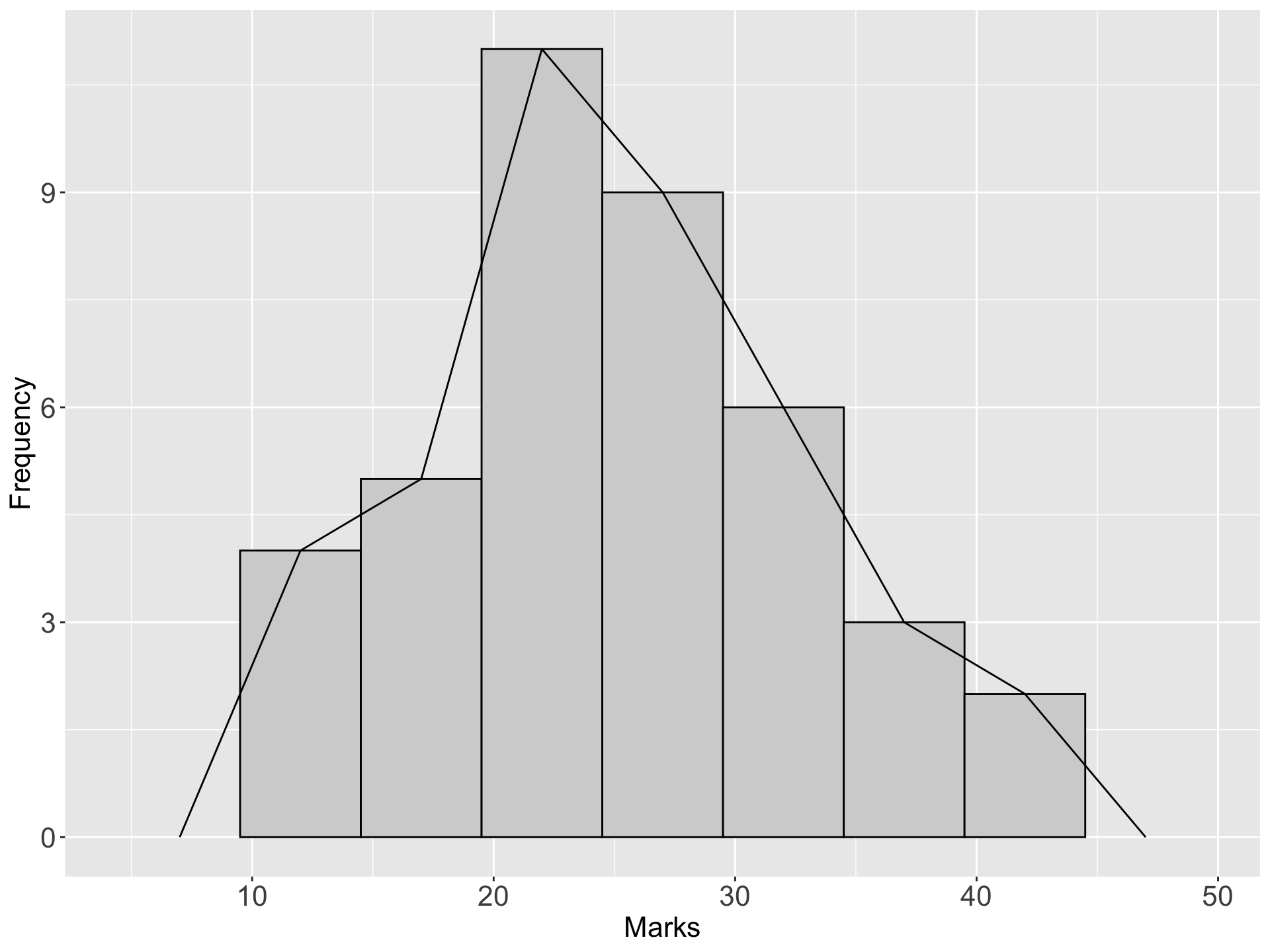
III Frequency polygon

If the mid-point of the top of each block in a histogram is joined by a straight line, a frequency polygon is produced.
This is done under the assumption that the frequencies in a class-interval are evenly distributed throughout the class

Example: The marks(out of 50) of a group of students are recorded in the accompanying table. Draw a frequency polygon for the data

Marks	Number of students
10 - 14	4
15 - 19	5
20 - 24	11
25 - 29	9
30 - 34	6
35 - 39	3
40 - 44	2
Total	40

IV Frequency curve

A frequency curve is drawn by smoothing the frequency polygon.
It is smooth in such a way that the sharp turns are avoided

Example: The marks(out of 50) of a group of students are recorded in the accompanying table. Draw a frequency curve for the data

Marks	Number of students
10 - 14	4
15 - 19	5
20 - 24	11
25 - 29	9
30 - 34	6
35 - 39	3
40 - 44	2
Total	40

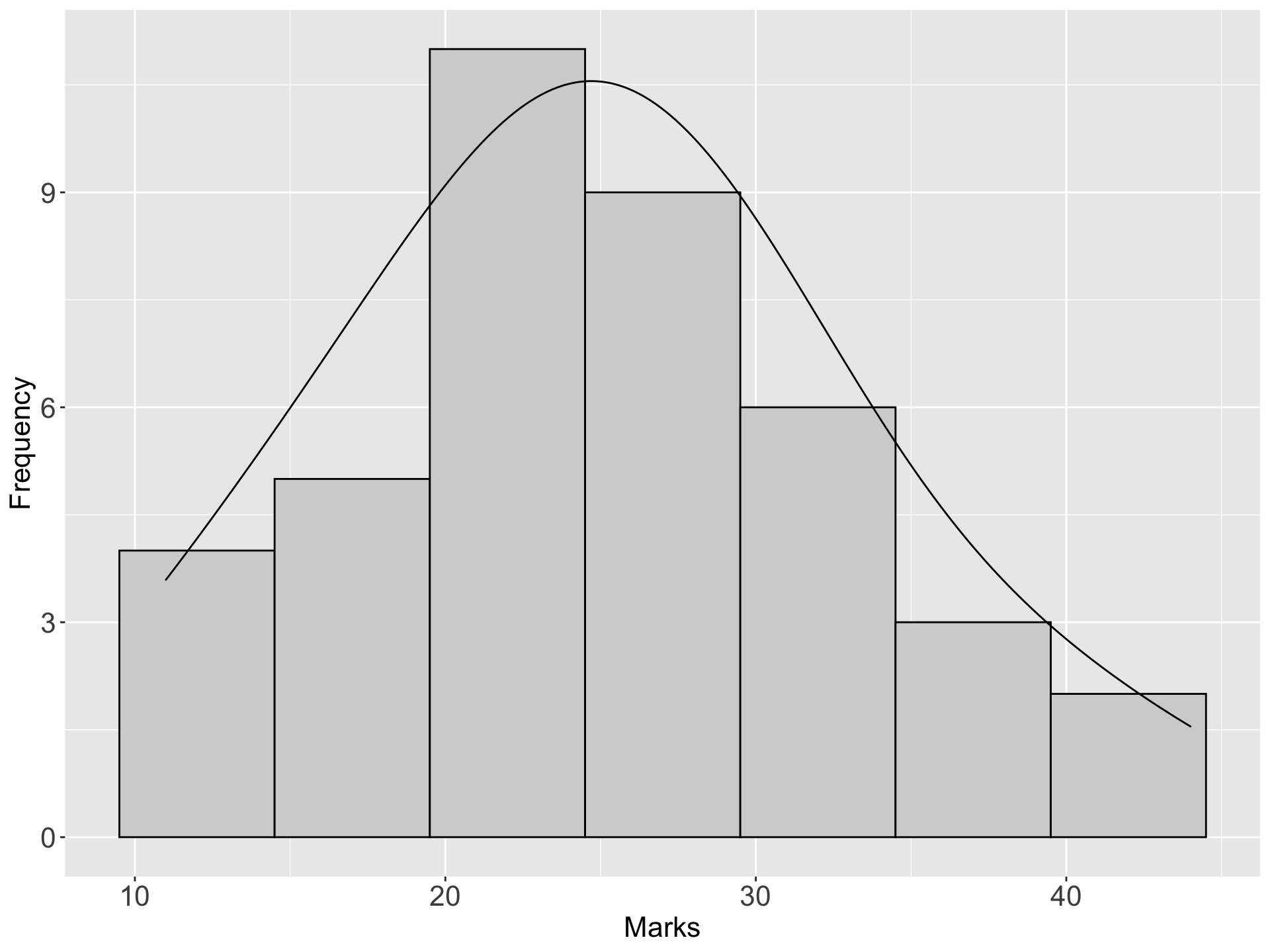
frequency curves arising in practice take on certain characteristics shapes as shown bellow

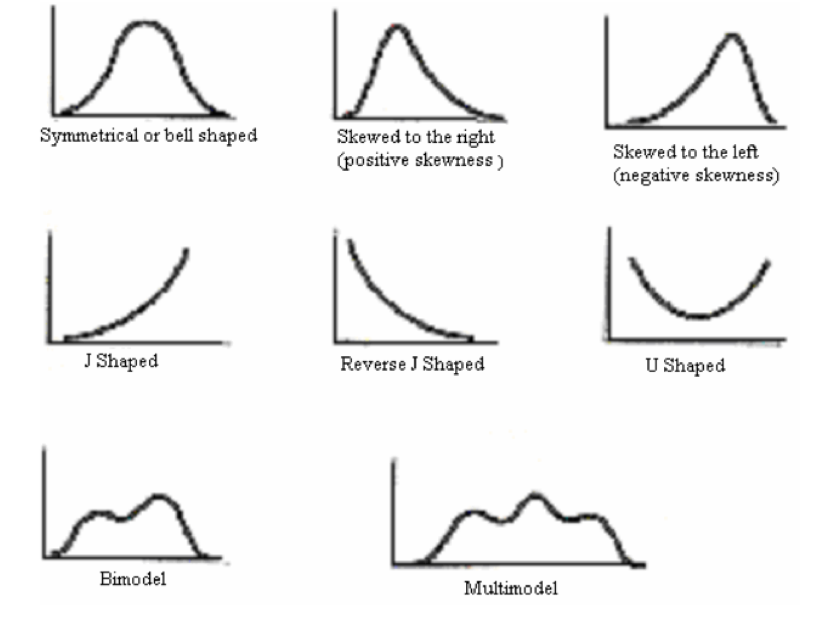
The symmetrical or bell shaped frequency curves are characterized by the fact that observations equidistant from the central maximum have the same frequency. An important example is the normal curve.
In the moderately asymmetrical or skewed frequency curves the tail of the curve to one side of the central maximum is longer than that to the other. If the longer tail occurs to the right the curve is said to be skewed to the right or to have positive skewness.While if the reverse is true the curve is said to be skewed to the left or to have negative skewness.
In a J shaped or reverse J shaped curve a maximum occurs at one end.
A U shaped frequency curve has maxima at both ends.
A bimodal frequency curve has two maxima. These appear as two distinct peaks (local maxima) in the frequency curve.When the two modes are unequal the larger mode is known as the major mode and the other as the minor mode.
A multimodal frequency curve has more than two maxima.

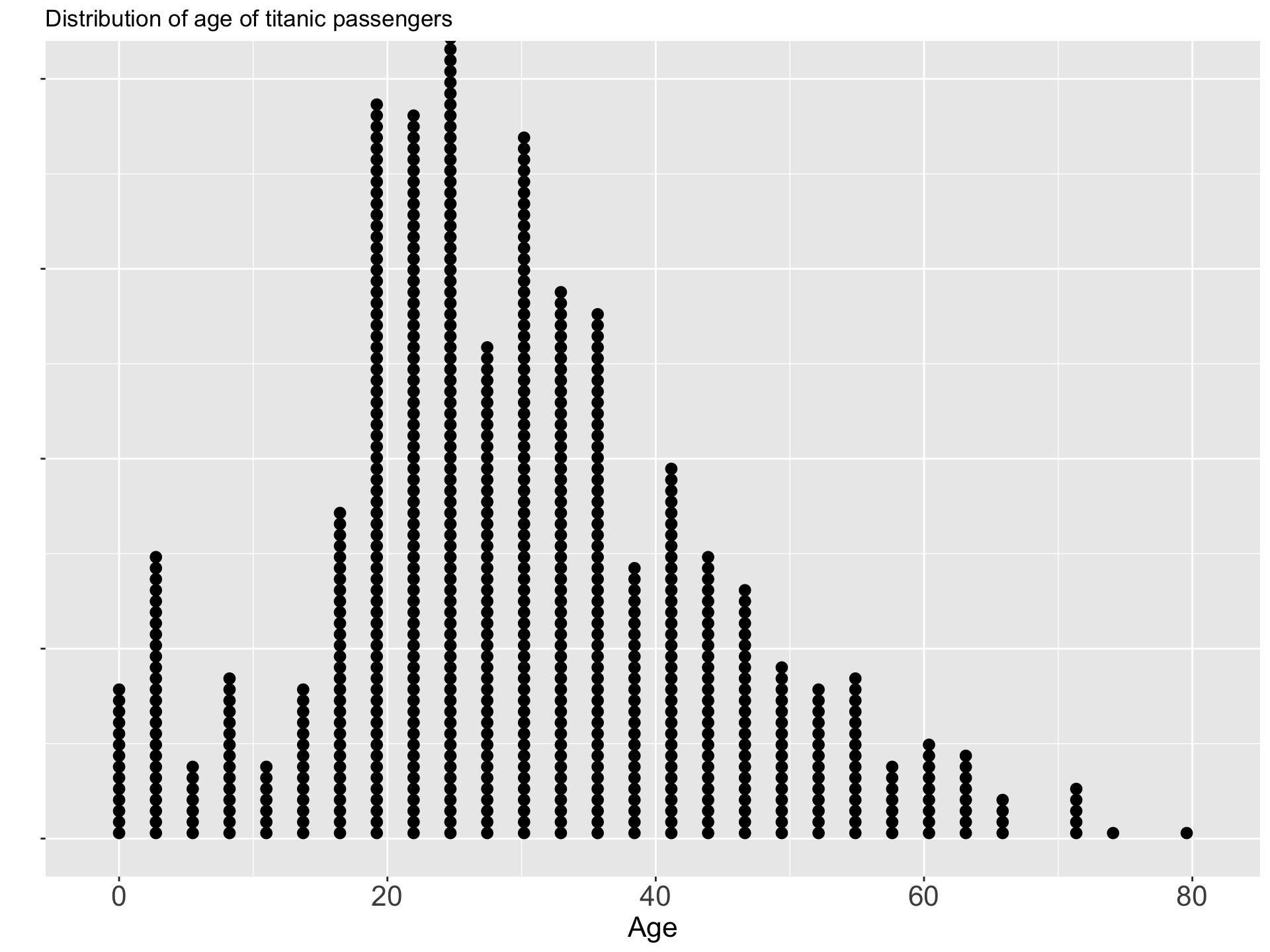
V Dot Plot

A dot plot is a method of presenting data which gives a rough but rapid visual appreciation of the way in which the data are distributed
It consists of a horizontal line marked out with divisions of the scale on which the variable is being measured -This graph can be used to represent only the numerical data.

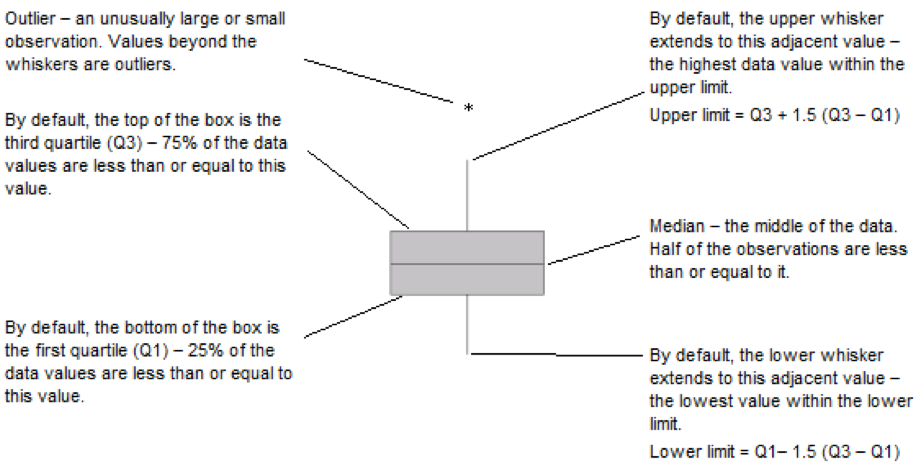
VI Box plot (Box and whisker plot)

Box plot is also a useful method of representing the behavior of a data set or comparing two or more data sets.
Box plot is constructed by identifying five statistics from the data set as largest value, smallest values, median, Q1 and Q3.

Example:

Construct a box plot for the following data set (Marks of students)

\[\text{52, 88, 56, 79, 72, 91, 85, 88, 68, 63, 76, 73, 86, 95, 12, 69}\]

Xmin = 12 Xmax = 95 Q1 =64.25 Q2 = Median = 74.5 Q3 = 87.5

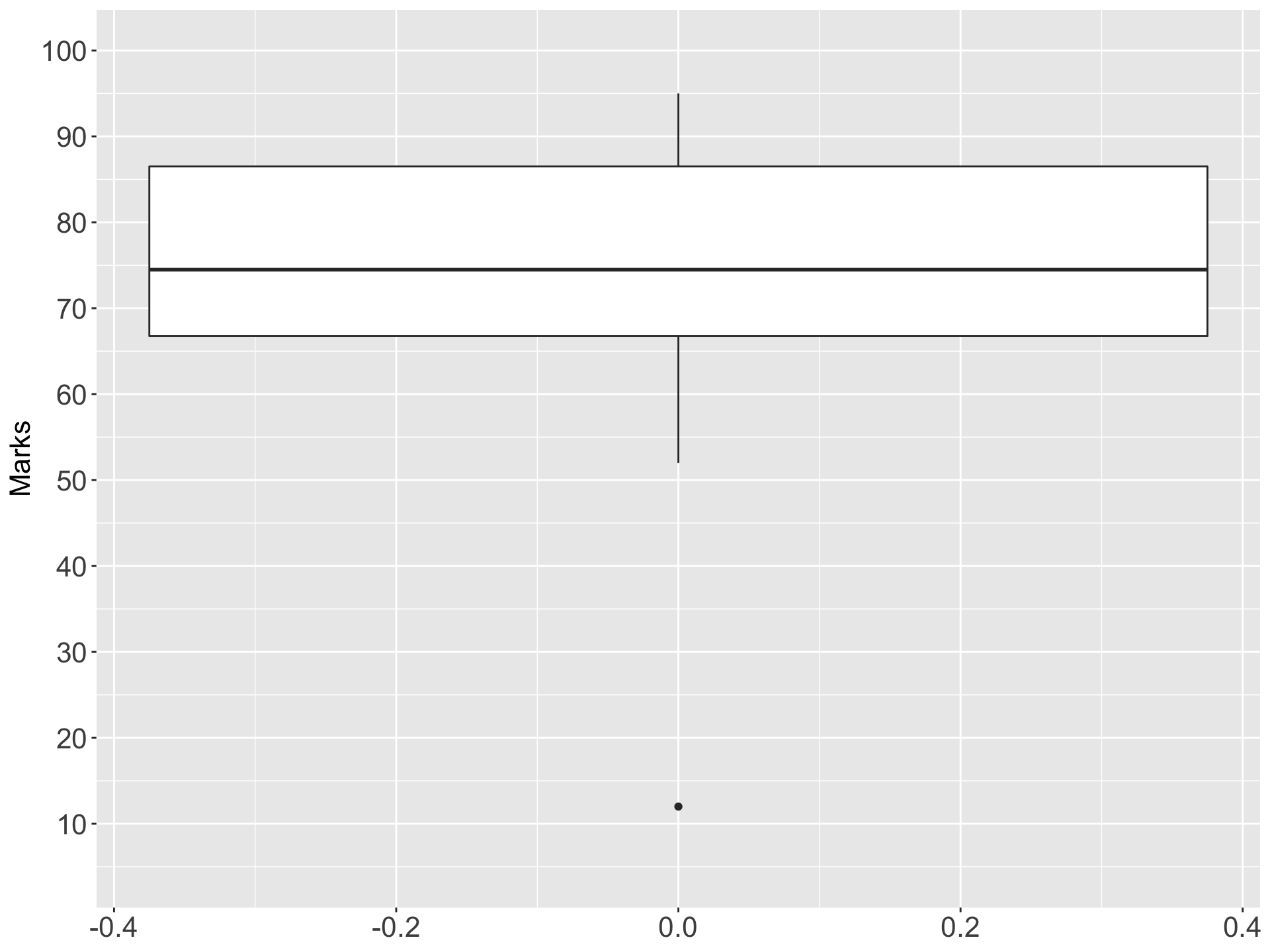
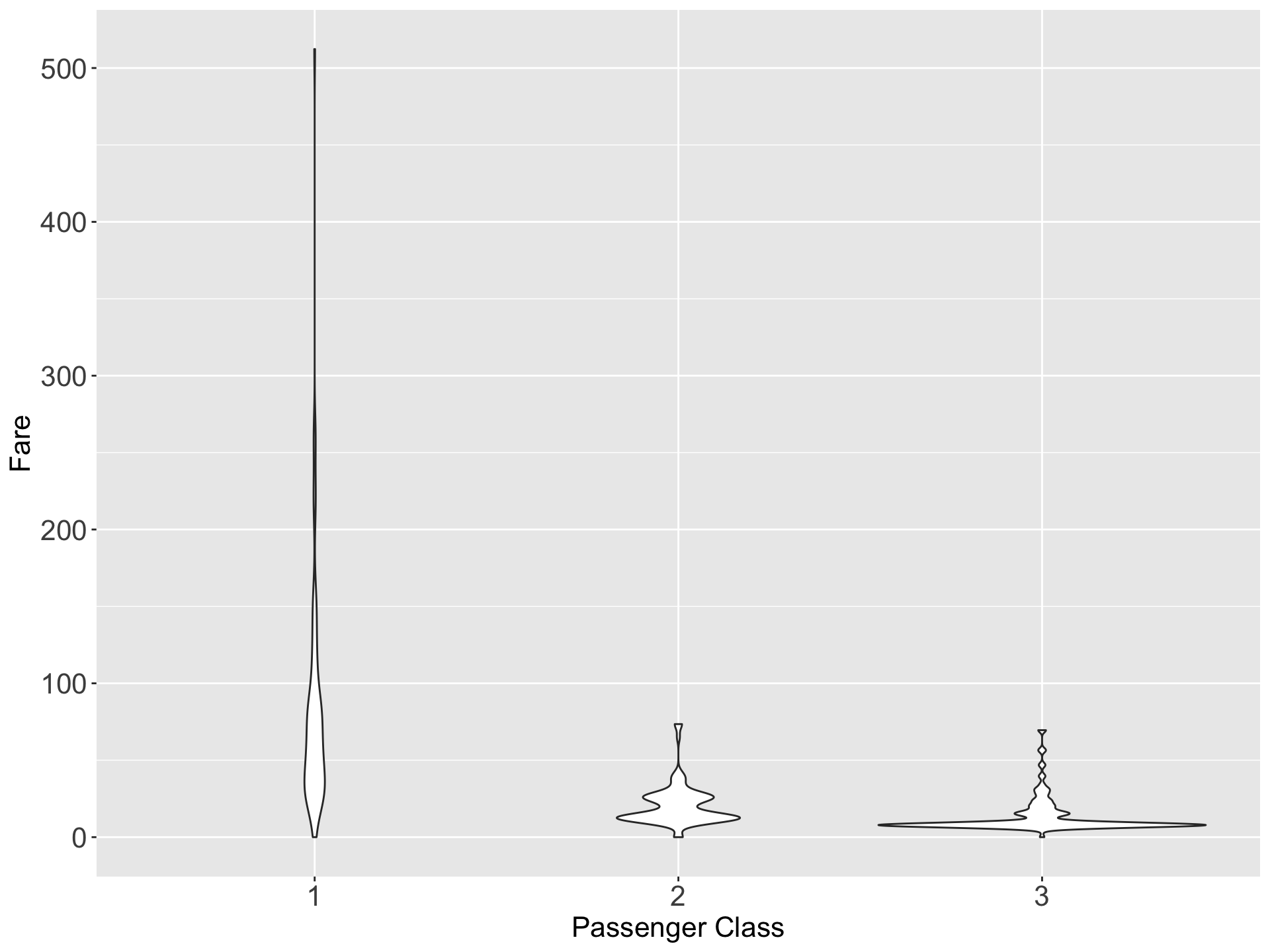
VII Violin plot

A violin plot is a method of plotting quantitative data.
It is similar to a box plot, with the addition of a rotated kernel density plot on each side.
Violin plots are similar to box plots, except that they also show the probability density of the data at different values, usually smoothed by a kernel density estimator.

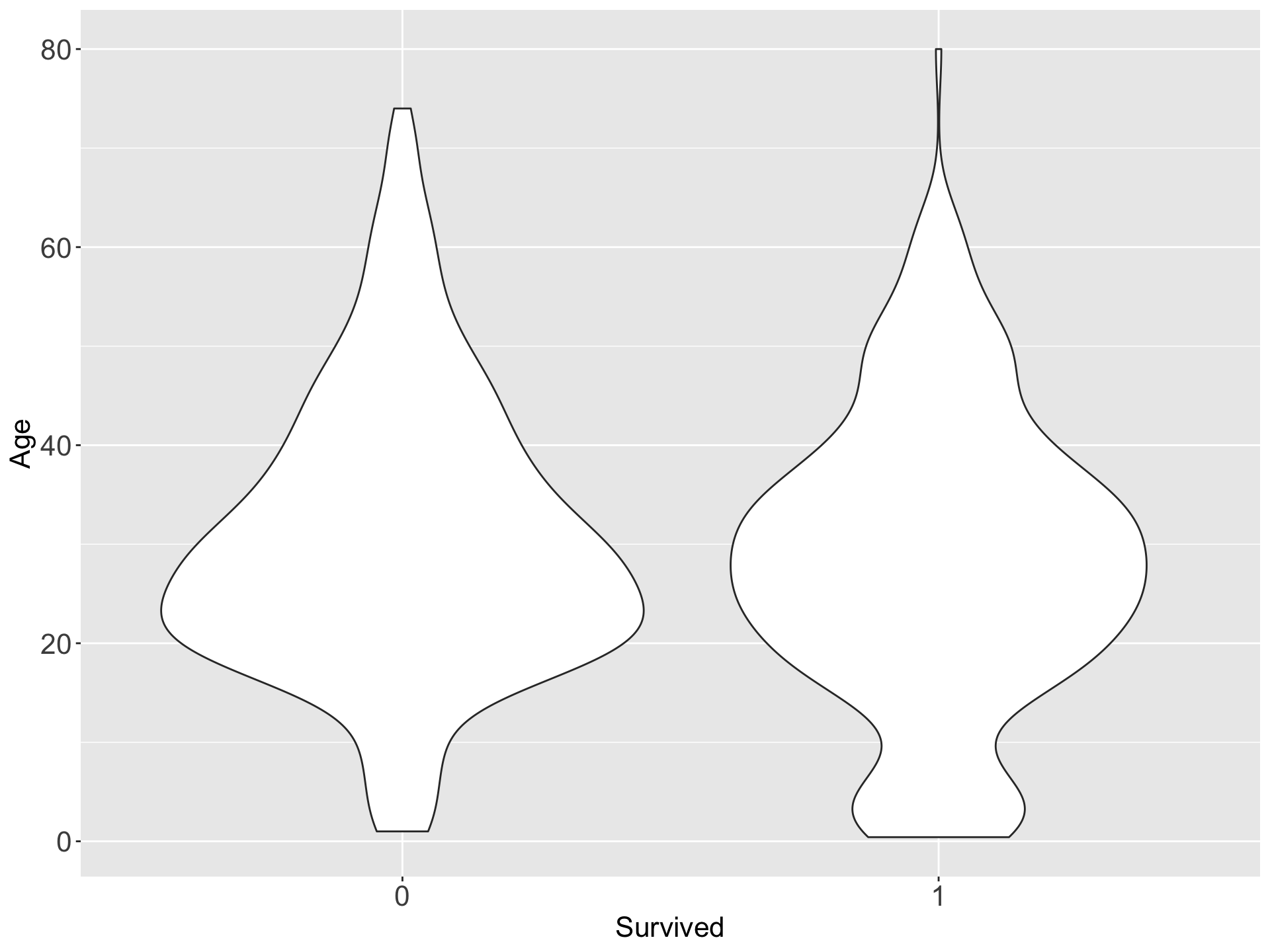
6.3 Summary Measures

Although frequency distribution serves useful purpose, there are many situations that require other types of data summarization.
What we need in many instances is the ability to summarize the data by means of a single number called a descriptive measure.
Descriptive measures may be computed from the data of a sample or the data of a population. To distinguish between them we have the following definitions.

Definitions

A descriptive measure computed from the data of a sample is called a statistic.
A descriptive measure computed from the data of a population is called a parameter.

6.3.1 Measures of Central Tendency

Measure of central tendency yield information about the center, or middle part, of a group of numbers.
Eg: Mode, Median, Arithmetic Mean, Geometric mean, Harmonic Mean, Quadratic Mean, Quartiles, Deciles, and Percentiles

6.3.1.1 Mode

The Mode is the most frequently occuring value in a set of data
Organizing the data into an ordered array (an ordering of the numbers from smallest to largest) helps to locate the mode.
A series having only one mode is called as uni-modal
In the case of a tie for the most frequent occuring value, two modes are listed. Then the data are set to be bimodal
If a set of data is not exactly bimodal but contains two values that are more dominant than others, some researchers take the liberty of referring to the data set as bimodal even without an exact tie for the mode.
Data sets with more than two modes are referred to as multimodal.
The mode is an appropriate measure of central tendency for nominal-level data.
The mode can be used to determine which category occurs most frequently.

For ungrouped data

Example 01: Find mode of the following datasets

Dataset 1: 12, 14, 10, 8, 6, 8, 15, 8

Dataset 2: 40, 44, 57, 48, 78

Dataset 3: 42, 45, 55, 50, 45, 40, 55, 45, 52, 55, 54

For grouped frequency data

Example 02: Find mode of the following data

Marks	Number of students
20	8
30	10
40	16
50	8
60	5
70	3

Advantages and disadvantages of mode

Advantages

Easy to understand
Easy to calculate
Not affected by extreme values in the dataset
Good for qualitative data

Disadvantages

Not suitable for further mathematical calculations
There may be more than one mode for a given dataset
It is not based upon all the observations
In some cases, we may not be able to find a mode for a given dataset

6.3.1.2 Median

The median is the middle value in an ordered array of numbers.
Median divides the series into equal parts
The following steps are used to determine the median.
STEP 1: Arrange the observations in an ordered data array.
STEP 2: For an odd number of terms, find the middle term of the ordered array. It is the median.
STEP 3: For an even number of terms, find the arithmetic mean of the middle two terms. This arithmetic mean is the median.

\[Median = \text{the }(\frac{n+1}{2})\text{th item in the data array} \]

The level of data measurement must be at least ordinal for a median to be meaningful.

Example 1: Find the median of the dataset 1, 8, 6, 3, 2

Example 2: Find the median of the dataset 8, 9, 1, 2, 14, 12

Advantages and disadvantages of median

Advantages

Simple to understand
Easy to calculate
Not affected by extreme values in the dataset
Can be calculated even for qualitative variables (ordinal scale data)

Disadvantages

It is not based upon all the observations

6.3.1.3 Arithmetic Mean

The arithmetic mean (usually called mean) is the sum of all observations divided by the total number of observations.
Population Mean
- The poupulation mean us represented by the Greek letter $mu$ ($\mu$).
- Let, $N$ is the number of terms in the population.

\[\mu = \frac{\sum{x}}{N}=\frac{x_1+x_2+x_3+...+x_N}{N}\]

Sample Mean
- The sample mean is represented by $\bar{x}$
- Let, $n$ is the number of terms in the sample \[\bar{x} = \frac{\sum{x}}{n}=\frac{x_1+x_2+x_3+...+x_n}{n}\]
It is inappropriate to use the mean to analyse data that are not at least interval level in measurement.

Example 1: Calculate the mean from the following data

Student	1	2	3	4	5	6	7	8	9	10
Marks	40	50	53	78	58	60	73	35	43	48

Advantages and disadvantages of arithmetic mean

Advantages

Simple to understand
Easy to calculate
Based on all the observations
Well defined
Unique
Can be used in further calculation

Disadvantages

Can be affected by extreme values in the dataset
May lead to false conclusions
Only applicable to quantitative data (not applicable to qualitative data)

Empirical relationship between mean, mode, median

In case of symmetrical distribution, mean, median and mode coincide $(mean = meadian= mode)$

For a moderately asymmetrical distribution, the following relationship exists $Mean – Mode = 3(Mean - Median)$

Choice between mean and median

Mean is very sensitive to outliers.Median is not sensitive to outliers
When there are outliers in a data set, median is more appropriate than mean

6.3.1.4 Quartiles, Deciles and Percentiles

Median divides the data set into two equal parts.
There are other values which divide the data set into a number of equal parts
Those are Quartiles, Deciles and Percentiles

(a) Quartiles (Q) – Quartiles divide an array into four equal parts

\[Q_i = \text{the }\frac{i}{4}(n+1)\text{th item in the data array} \]

(b) Deciles (D) – Deciles divide an array into ten equal parts

\[D_i = \text{the }\frac{i}{10}(n+1)\text{th item in the data array} \]

(c) Percentiles (P) – Percentiles divide an array into 100 equal parts

\[P_i = \text{the }\frac{i}{100}(n+1)\text{th item in the data array} \]

6.3.2 Measures of Variability

Measure of central tendency yield information about particular points of a data set.
However, business researchers can use another group of analytic tools to describe a set of data.
These tools are measures of variability, which describe the spread or the dispersion of a set of data.
Using measures of variability in conjunction with measures of central tendency makes possible a more complete numerical description of the data.
This section focuses on seven measures of variability for ungrouped data: range, interquartile range, variance, standard deviation, z score and coefficient of variation.

6.3.2.1 Range

The range is the difference between the largest value of a data set and the smallest value.

\[Range = Maximum - Minimum\]

One important use of the range is in quality assurance, where the range is used to construct control charts
Advantages and disadvantages of range

Advantages

Easy to understand and calculate

Disadvantages

Consider only the highest and lowest values of the data and fails to take account of any other observations in the dataset
Heavily influenced by extreme values

6.3.2.2 Interquartile Range (IQR)

We use the interquartile range (IQR) to measure the spread of a data around the median (M).
The interquartile range is the range of values between the first and third quartile.
Essentially it is the range of the middle 50% of the data and is determined by computing the value of $Q_3 - Q_1$.
The interquartile range is especially useful in situations where data users are more interested in values towards the middle and less interested in extremes.
The interquartile range is used in the construction of box and whisker plots.
By eliminating the lowest 25% and the highest 25% of the items in a series, we are left with the central 50% , which are ordinarily free of extreme values.

Advantages

Easy to understand and calculate
Not influenced by extreme values

Disadvantages

Ignore the first $25\%$ and the last $25\%$ in the dataset

6.3.2.3 Variance and Standard Deviation

To measure the spread of data around the mean, we use the standard deviation (S).
The variance and standard deviation are two very popular measures of dispersion.
These measures are not meaningful unless the data are at least interval-level data.
Their formulations are categorized into whether to evaluate from a population or from a sample.

NOTE

Sum of deviations from the arithmetic mean is always zero. \[{\sum{(x-\mu)} = 0}\]
This property requires considering the alternative ways to obtain measure of variability.

6.3.2.3.1 Variance

The variance is the average of the squared deviations about the mean for a set of numbers.
The population variance is denoted by $\sigma^2$

\[\sigma^2 = \frac{\sum(x-\mu)^2}{N}\]

The sum of the squared deviations about the mean of a set of values - called the sum of squares of $x$ and sometimes abbreviated as $SS_x$
Because the variance is computed from squared deviations, the final result is expressed in terms of squared units of measurements.
Statistics measured in squared units are problematic to interpret.

6.3.2.3.2 Standard Deviation

The standard deviation is the square root of the variance.
The population standard deviation is denoted by $\sigma$

\[\sigma = \sqrt{\frac{\sum(x-\mu)^2}{N}}=\sqrt{\sigma^2}\]

One feature of standard deviation that distinguishes it from a variance is that the standard deviation is expressed in the same units as the raw data, whereas the variance is expressed in those units squared.

Advantages

Based on all the observations
Since this is based on arithmetic mean, it has all the merits of it
The most important and widely used measure of dispersion

Disadvantages

Not easy to understand and difficult to calculate
Gives more weight to extreme values, because the values are squared up

6.3.2.4 Empirical Rule

The empirical rule is an important rule of thumb that is used to state the approximate percentage of values that lie within a given number of standard deviations from the mean of a set of data if the data are normally distributed
The empirical rule is used only for three numbers of standard deviations: $1\sigma$, $2\sigma$, $3\sigma$

Distance from the mean	Values within distance
$\mu\pm1\sigma$	$68\%$
$\mu\pm2\sigma$	$95\%$
$\mu\pm3\sigma$	$99.7\%$

If a set of data is normally distributed, or bell shaped, approximately $68\%$ of the data values are within one standard deviation of the mean, $95\%$ are within two standard deviations, and almost $100\%$ are within three standard deviations.

6.3.2.5 Population versus sample variance and standard deviations

The sample variance is denoted by $s^2$ and the sample standard deviation by $s$.
The main use for sample variances and standard deviations is as estimators of population variances and standard deviations.
Thus, computation of the sample variance and standard deviation differs slightly from computation of the population variance and standard deviation.
Both the sample variance and sample standard deviation use $n-1$int he denominator instead of $n$ because using $n$ in the denominator of a sample variance results in a statistic that tends to underestimate the population variance.
While discussion of the properties of good estimator is beyond the scope of this course, one of the properties of a good estimator is being unbiased.
Whereas, using $n$ in the denominator of the sample variance makes it a biased estimator, using $n-1$ allows it to be an unbiased estimator, which is a desirable property in inferential statistics.

Sample variance

\[s^2 = \frac{\sum{(x-\bar{x})^2}}{n-1}\]

Sample standard deviation

\[s = \sqrt{\frac{\sum{(x-\bar{x})^2}}{n-1}}= \sqrt{s^2}\]

6.3.2.6 Computational formulas for variance and standard deviation

An alternative method of computing variance and standard deviation, sometimes referred to as the computational method or shortcut method, is available.
Algebraically,

\[\sum{(x-\mu)^2}= \sum{x^2}- \frac{(\sum x)^2}{N}\]

and

\[\sum{(x-\bar{x})^2}= \sum{x^2}- \frac{(\sum x)^2}{n}\]

Substituting these equivalent expressions into the original formulas for variance and standard deviation yields the following computational formulas.

Computational formula for population variance and standard deviation

\[\sigma^2 = \frac{\sum{x^2}- \frac{(\sum x)^2}{N}}{N}\]

\[\sigma = \sqrt{\sigma^2}\]

Computational formula for sample variance and standard deviation

\[s^2 = \frac{\sum{x^2}- \frac{(\sum x)^2}{n}}{n-1}\]

\[s = \sqrt{s^2}\]

For situations in which the mean is already computed or is given, alternative forms of these formulas are:

\[\sigma^2 = \frac{\sum{x^2}-N\mu^2}{N}\]

\[s^2 = \frac{\sum{x^2}-n(\bar{x})^2}{n-1}\]

6.3.2.7 Coefficient of variation

In general, for two variables measured with he same units (eg: two groups of people both weighed in kg), the group with the larger variance and standard deviation has n=more variability among their scores.
The unit of measure affects the size od the variance.
The same population weights, expressed in ‘grams’ rather than kg would have a larger variance and standard deviation.
The coefficient of variation, a measure of relative variability gets around this difficulty and makes it possible to compare variability across variables measured in different units.
The coefficient of variation is the ratio of the standard deviation to the mean, expressed as a percentage and is denoted CV.

\[CV = \frac{\sigma}{\mu}(100)\]

Using median and quartile deviation

\[CV = \frac{\frac{Q_3 - Q_1}{2}}{Median}(100)\]

The coefficient of variation essentially is a relative comparison of a standard deviation to its mean.
The coefficient of variation can be useful in comparing standard deviations that have been computed from data with different means.
The choice of whether to use a coefficient of variation or raw standard deviations to compare multiple standard deviations is a matter of preference
The coefficient of variation also provides and optional method of interpreting the value of a standard deviation.

6.3.3 Measures of Shape

Measures of shape are tools that can be used to describe the shape of a distribution of data.
In this section, we examine two measures of shapes: skewness and Kurtosis.

6.3.3.1 Skewness

A distribution of data in which the right half is a mirror image of the left half is said to be symmetrical.
One example of a symmetrical distribution is the normal distribution, or bell curve.
Skewness is a measure of symmetry, or more precisely, the lack of symmetry
The measures of asymmetry are called as measures of skewness.
The skewed portion is the long, thin part of the curve

Skewness and the relationship of the mean, median and mode

The concept of skewness helps us to understand the relationship between the mean, median and mode.
In a unimodal distribution (distribution with a single peak or mode) that is skewed, the mode is the apex (high point) of the curve and the median is the middle value.
The mean tends to be located toward the tail of the distribution, because the mean is affected by all values, including the extreme ones.
A bell-shaped or normal distribution with the mean, median and mode all at the centre of the distribution has no skewness.

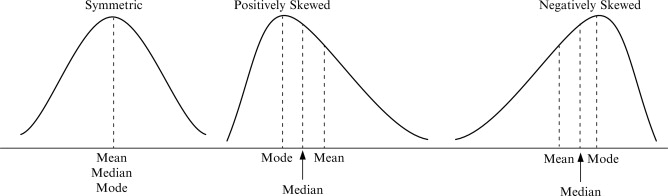
Figure 6.1: Relationship of mean, median and mode for different types of skewness

6.3.3.1.1 Pearsonian coefficient of skewness

This coefficient compares the mean and median in light of the magnitude of the standard deviation

\[S_k = \frac{3(\mu-M_d)}{\sigma}\]

where $S_k$ = coefficient of skewness, $M_d$ = median

Note that if the distribution is symmetrical, the mean and median are the same value and hence the coefficient of skewness is equal to zero.
If the value of $S_k$ is positive, the distribution is positively skewed.
If the value of $S_k$ is negative, the distribution is negatively skewed.
The greater the magnitude of $S_k$, the more skewed is the distribution.

6.3.3.2 Kurtosis

Kurtosis describes the amount of peakedness of a distribution.
Kurtosis is a measure of whether the data are peaked or flat relative to a normal distribution
Distributions that are high and thin are referred to as leptokurtic distributions.
Distributions that are flat and spread out are referred to as platykurtic distributions.
Between the above two types are distributions that are more ‘normal’ in shape, referred to as mesokurtic distributions

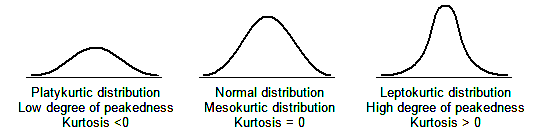
Figure 6.2: Types of kurtosis

6.3.4 Measures of Association

Many times in business it is important to explore the relationship between two numerical variables
Measures of association are statistics that yeild information about the relatedness of numerical variables.
In this section, we discuss only one measure of association, correlation, and do so only for two numerical variables.

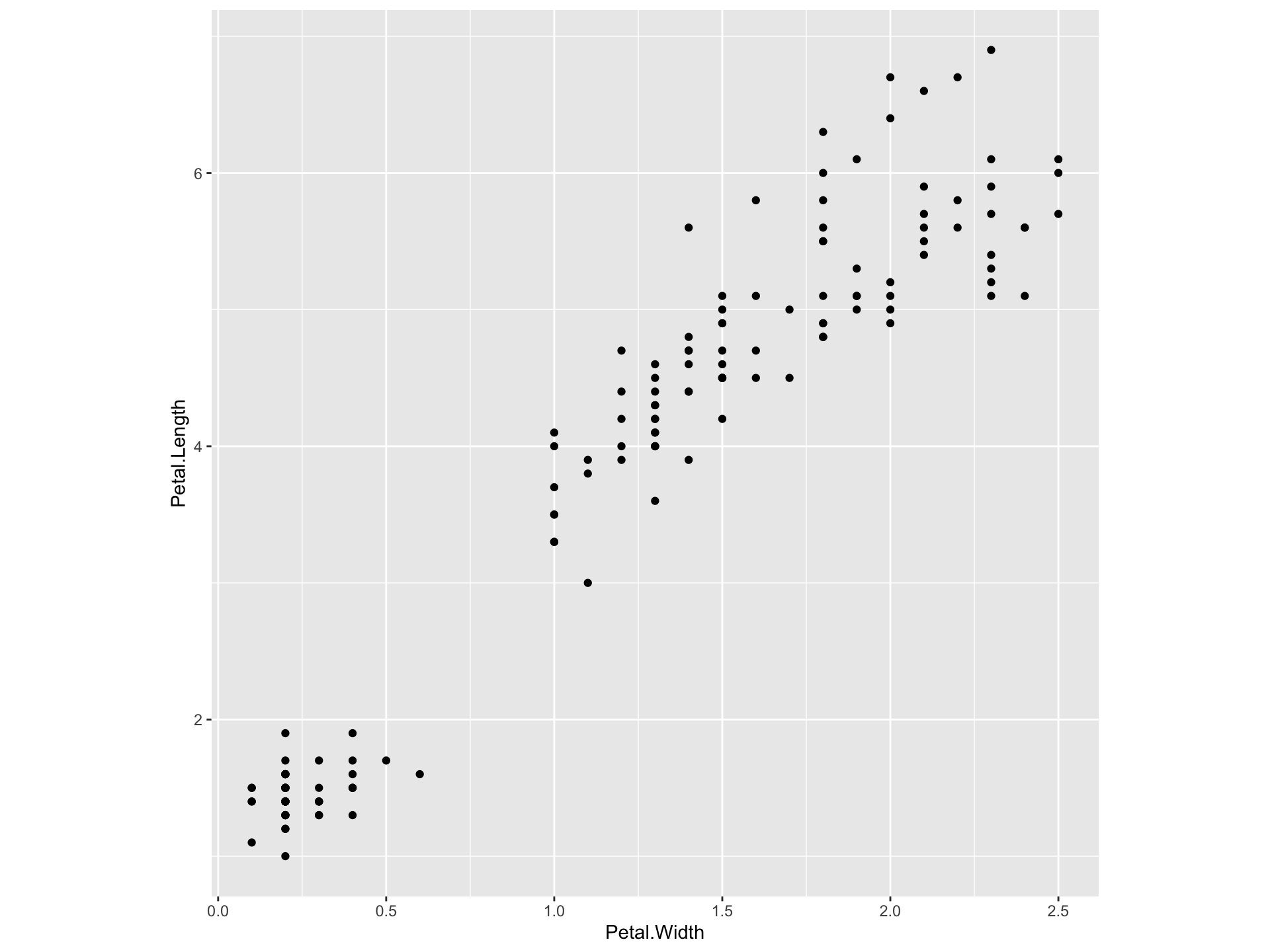
6.3.4.1 Scatter plot

A scatter plot is a two dimensional graph of pairs of points from two numerical variables
In a quantitative bi-variate dataset, we have a $(x,y)$ pair for each sampling unit, where $x$ denotes the independent variable and $y$ denotes the dependent variable.
Each $(x,y)$ pair can be considered as a point on the Cartesian plan.
Scatter plot is a plot of all the $(x,y)$ pairs in the dataset.
The purpose of scatter plot is to illustrate any relationship between two quantitative variables.
- If the variables are related, what kind of relationship it is, linear or nonlinear?
- If the relationship is linear, the scatter plot will show whether it is negative or positive.

Example: Edgar Anderson’s Iris Data

This famous (Fisher’s or Anderson’s) iris data set gives the measurements in centimeters of the variables sepal length and width and petal length and width, respectively, for 50 flowers from each of 3 species of iris. The species are Iris setosa, versicolor, and virginica.

6.3.4.2 Correlation

Correlation is a measure of the degree of relatedness of two or more variables.
Several measures of correlation are available , the selection of which depends mostly on the level of data being analysed.
Ideally, researchers would like to calculate $\rho$, the population coefficient of correlation.
However, because researchers virtually always deal with sample data, this section introduces a widely used sample coefficient of correlation, $r$.
This measure is applicable only if both variables being analysed have at least an interval level of data

Pearson product-moment correlation coefficient ($r$)

The statistic $r$ is the Pearson product-moment correlation coefficient, named after Karl Pearson (1857 - 1936).
The tern $r$ is a measure of the linear correlation of two variables.
It is a number that ranges from -1 to 0 to +1, representing th strength of the linear relationship between the variables.
An $r$ value of $+1$ denotes a perfect linear positive relationship between two variables.
An $r$ value of $-1$ denotes a perfect linear negative relationship between two variables, which indicates an inverse relationship between two variables: as one variable gets larger, the other gets smaller.
An $r$ value of 0 means no linear relationship is present between the two variables.

\[ r = \frac{\sum(x-\bar{x})(y-\bar{y})}{\sqrt{\sum(x-\bar{x})^2\sum(y-\bar{y})^2}}\]

\[ r = \frac{\sum{xy} - \frac{(\sum x\sum y)}{n}}{\sqrt{[\sum{x^2- \frac{(\sum{x})^2}{n}}][\sum y^2-\frac{(\sum y)^2}{n}]}}\]

Examples: Following figure shows five different degrees of correlation:

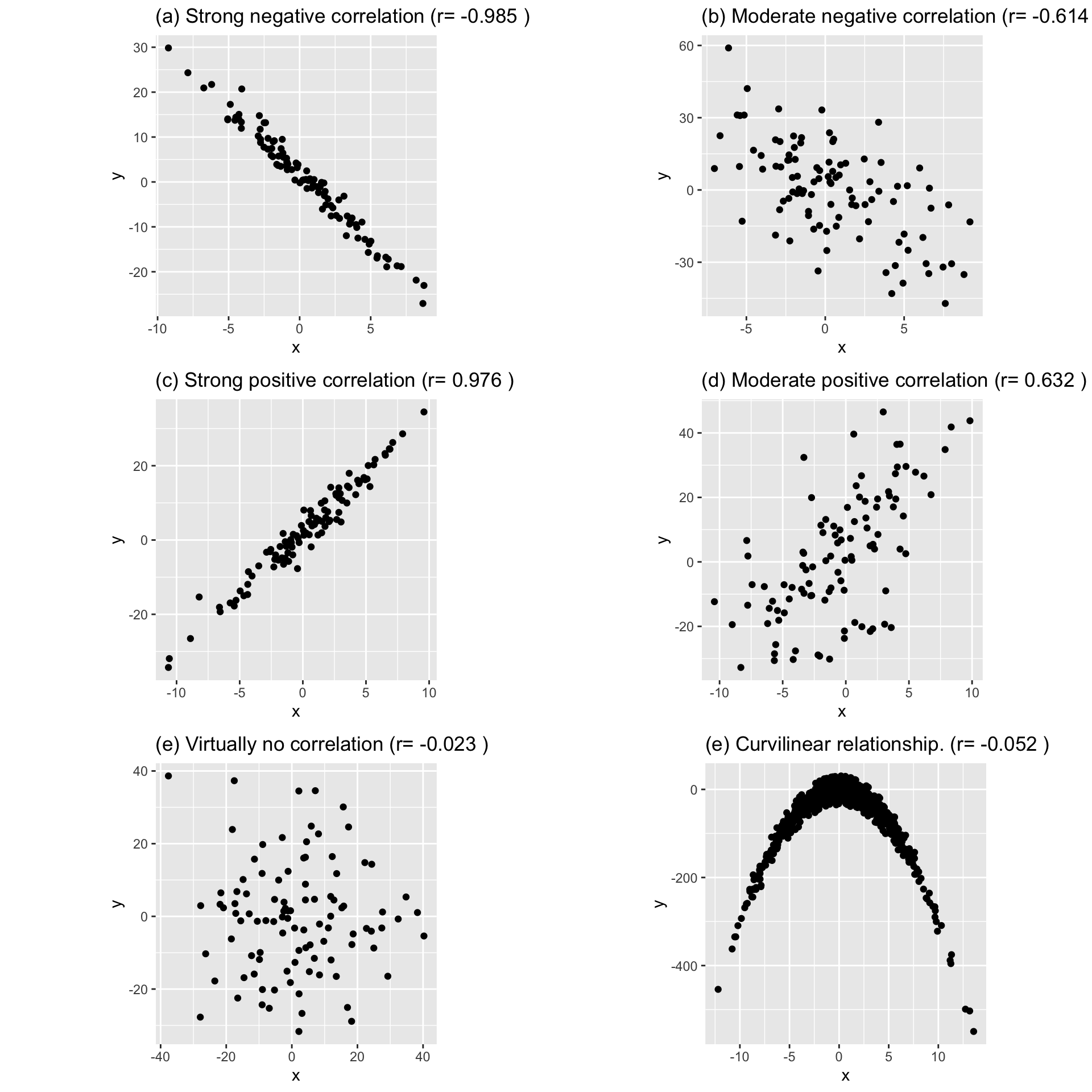
NOTE

When $r=0$, it signifies there is no linear relationship between the two variables. (There can be a non-linear relationship, Figure (e))
Figure (e): There is a very strong curvilinear relationship. But there is no linear relationship.

6.4 Tutorial

Chapter 6: Descriptive Statistics

A power company in Sri Lanka designs and manufactures power distribution switchboards for hospitals, bridges, airports, highways and water treatment plants. Power company marketing director wants to determine client satisfaction with their products and services. He developed a questionnaire that yields a satisfaction score between 0 and 100 for participant responses. A random sample of 50 of the company’s 1000 clients is asked to complete a satisfaction survey. The satisfaction scores for the 50 participants are averaged to produce a mean satisfaction score.

What is the objective of this study?
What is the population for this study?
What is the sample for this study?
What is the statistic for this study?
What would be a parameter for this study?

Determine the type and the scale of measurement of the following variables

The time required to produce an item on an assembly line
the number of litres of milk a family drinks in a week
The ranking of 50 students in your class after their overall performance have been designated as excellent, good, satisfactory or poor
The telephone area code of clients in Australia
The age of each of your batch mates
The sales at the local pizza restaurant each month
A student index number
The response time of emergency services
The number of tickets sold at a ticket counter on any given day
Monthly maximum air temperature

The grades of 30 students for Statistics are as follows:

B, C, B, D, B, C, C, A , B, C,

C, B, E, B, B, D, D, F, B, D,

D, A, B, A, B, C, E, A, A, E

Construct a frequency table with suitable values (eg: absolute frequency, relative frequency, cumulative frequency, cumulative relative frequency)

The gender type of a group of 10 students are as follows:

Male, Female, Female, Male, Female Female, Male, Male, Female, Female

Construct a frequency table with suitable values (eg: absolute frequency, relative frequency, cumulative frequency, cumulative relative frequency )

In a study conducted to investigate the relationship between delivery time and computer-assisted ordering, the following data were gathered from a sample of 40 firms, that 16 use computer-assisted ordering, while 24 do not. Furthermore, past data are used to categorize each firm’s delivery times below the industry average, equal to the industry average, or above the industry average. The results obtained are given in the table below.

Computer Assisted Ordering	Delivery Time Below Industry Average	Delivery Time Equal to Industry Average	Delivery Time Above industry Average	Row Total
No	4	12	8	24
Yes	10	4	2	16
Total	14	16	10	40

For each row and column total, calculate the corresponding row or column percentage.
For each cell, calculate the corresponding cell, row, and column percentages.
Carry out graphical analysis to investigate the relationship between delivery-time performance and computer-assisted ordering.
What conclusions can be made about the nature of the relationship?

Giving suitable examples distinguish between multiple bar chart and a component bar chart.
Write down advantages and disadvantages of each chart and when they should be used

In a study conducted to investigate the effect of wearing helmets in riding motorcycles to reduce the head injuries, the following data were gathered by investigating 151 motorcycle accidents reported during last 10 month period. Out of the total number of cases (151) investigated, only 102 people were wearing helmets properly at the time of the accidents. Out of them, only 9 got severe head injuries. The rest got either minor head injuries or no head injuries at all. Among 49 who were not wearing helmets at the time of the accident, 15 got server head injuries and the rest got minor head injuries or no head injuries at all.

Use an appropriate table to represent the above data and state what conclusions can be drawn from it
Carry out a suitable graphical analysis to investigate the effect of wearing helmets in riding motorcycles to reduce the head injuries.

The table below shows a frequency distribution of the weekly wages of 65 employees at the ABC Company. With reference to this table,

Wages (in $)	Number of Employees
250.00 - 259.99	8
260.00 - 269.99	10
270.00 - 279.99	16
280.00 - 289.99	14
290.00 - 299.99	10
300.00 - 309.99	5
310.00 - 319.99	2
Total	65

Construct a histogram
Construct a frequency polygon
Construct a frequency curve
State what conclusions can be drawn from the above graphical analysis

The contribution of the agriculture, industrial, and service sector to the Gross Domestic Product (GDP) for each province in Sri Lanka is given in the table below. It is required to investigate whether the contributions are varying from province to province. What kind of graph you would suggest for representing data to serve the purpose. Justify your answer. Sketch the proposed graph.

Marks of 16 students are given below.

\[\text{52, 88, 56, 79, 72, 91, 85, 88, 68, 63, 76, 73, 86, 95, 12, 69}\]

Find the quartile of the distribution and interpret the values
Construct a box plot for the data set
Are there outliers in the data set?

Listed below, ordered from smallest to largest, is the time in days the customers take to pay their invoices.

\[13, 13, 13, 20, 26, 27, 31, 34, 34, 34, 35, 35, 36, 37, 38, 41, 41, 41, 45, 47, 47, 47, 50, 51, 53, 54, 56, 62, 67, 82\]

Determine the median
Determine the first and third quartiles
Determine the 2nd decile and the 8th decile
Determine the 67th percentile

What are outliers?
Which of the following is/are unaffected by outliers? Underline the correct answer/ answers.

Mean
Median
Mode
Range
Standard deviation
Inter-quartile range

Some summary measures of a variable is given below. Descriptive Statistics:

N	Mean	StDev	Minimum	Q1	Median	Q3	Maximum
50	5.389	0.997	3.150	4.658	5.350	6.020	8.600

Are there outliers in this data set? YES/NO Justify your answer using a box plot

The mean and the standard deviation of 250 observations of a variable X are 62.1 and 4.3 respectively. However, in a re-scrutinizing process, it was found that the observations 72 and 81 were incorrectly recorded as 92 and 87. Find the correct mean and standard deviation of the data set.
The weekly sales from a sample of AB company were organized into a frequency distribution. The mean of weekly sales was computed to be $105,900, the median $105,000, and the mode $104,500

Sketch the sales in the form of a smoothed frequency polygon. Note the location of the mean, median and mode on the X-axis
Is the distribution symmetrical, positively skewed, or negatively skewed? Explain.

Compare the variation of the annual incomes of executives with the variation of the incomes of unskilled employees. The sample information is given below.

Type	$\bar{x}$	$SD$
Executives	500,000	50,000
Unskilled employees	22,000	2,200

Marks for the course module AB and the corresponding lecture attendance of 10 students are given below

Student Number	1	2	3	4	5	6	7	8	9	10
Marks in course module AB	84	51	91	60	68	89	98	58	53	47
Lecture attendance	13	6	15	4	12	14	15	10	11	6

Draw a scatter plot for the above data
Calculate the coefficient of correlation
Comment on the relationship between the marks and the lecture attendance

References

Black, K., Asafu-Adjaye, J., Khan, N., Perera, N., Edwards, P., & Harris, M. (2007). Australasian business statistics. John Wiley & Sons.

Spiegel, M. R., & Stephens, L. J. (2017). Schaum’s outline of statistics. McGraw Hill Professional.

Data source: https://www.kaggle.com/varimp/a-mostly-tidyverse-tour-of-the-titanic ↩

Distance from the mean	Values within distance
\(\mu\pm1\sigma\)	\(68\%\)
\(\mu\pm2\sigma\)	\(95\%\)
\(\mu\pm3\sigma\)	\(99.7\%\)